Computer Organization
Computers have changed a lot in the hardware details over the decades, yet they are still using a fundamental architecture that hasn't changed very much at all.
Quiz Question Nr. 1
Which of the following is not part of a computer:
ALU
CPU
BLU
bus
RAM
clock
Quiz Question Nr. 2
The clock does the following:
Determines the speed of the processor
Determines the speed of the memory
Sets the timestamp for files and network I/O
Synchronizes with GPS satellites
all of the above
Binary Numbers
It may be surprising, but we can create any number we want out of just two digits, zero and one. These two binary digits are called bits.
Powers of Two
Essential to creating binary numbers is knowing your powers of two. You'll soon be able to create the following table quickly and reliably:
0 1 1 2 2 4 3 8 4 16 5 32 6 64 7 128 8 256 k 2k log2(n) n
Quiz Question Nr. 3
The binary equivalent of 5 is
5
10000
110
101
Quiz Question Nr. 4
The decimal equivalent of the binary number 1010 is
6
5
12
none of the above
Let's also try some of the following numbers:
- 20
- 40
- 80
- 127
- 255
- 67
- 115
- 49
- 48
There are some interesting observations to make about those numbers:
- What happens when a number is multiplied by two or a power of two?
- What does a number look like when it is a power of two?
- What does a number look like when it is near a power of two?
Characters, ASCII and Unicode
Once we have numbers, we can represent characters and text by simply numbering the characters.
- Typically, each character is represented in a fixed
width (1 byte or 2 bytes) or a small variety of widths. This
may require
leading zeros
- ASCII is very old, extremely well-supported, and limited to 256 characters
- Unicode is relatively modern (though decades old), still dodgy in its support, and has few practical limits (billions of characters).
- There are other odd issues to deal with, such as encoding of line-endings.
Here's
the ASCII Table
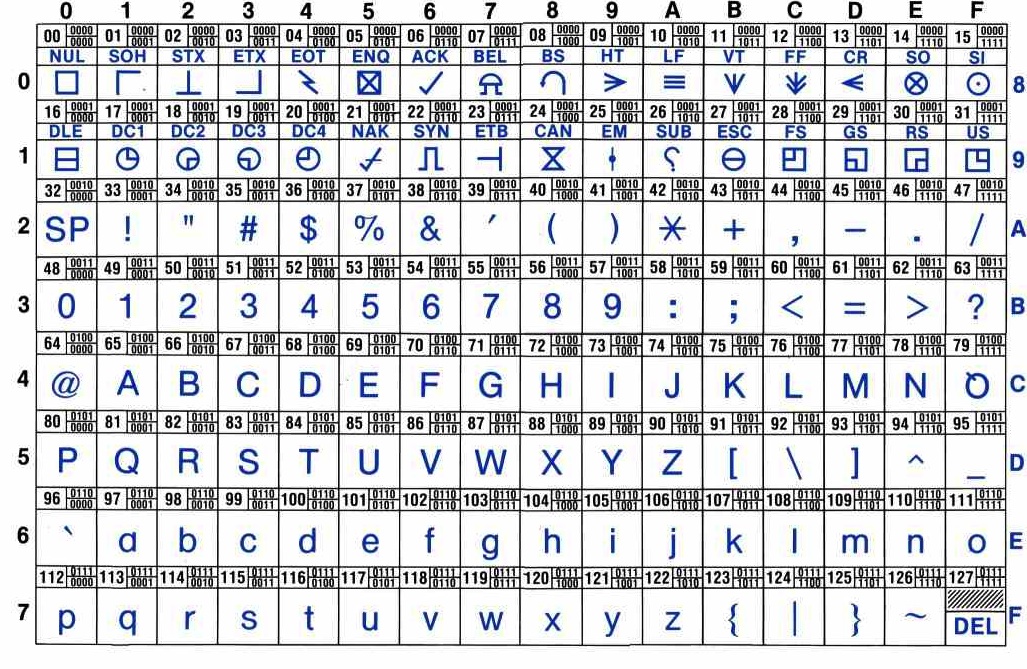
Quiz Question Nr. 5
What is 67 expressed as ASCII?
A
B
C
none of the above
What are 115, 49 and 48 expressed as ASCII?
Quiz Question Nr. 6
How many bits to represent the decimal number 1,000?
9
10
11
it can't be determined from the given information
Limited Number Representations
The fact that ASCII uses a limited number of bits has important implications. It can't represent an unbounded number of characters. This is true of all representations that use a limited number of bits.
- Did you hear about how Psy broke YouTube's view counter? That's because YouTube used a fixed-size counter.
- Did you hear that the internet is running out of IP addresses?
Quiz Question Nr. 7
It's happens to be the case
that .wellesley.edu is a "class B" domain, which
means all the IP addresses are of the form 149.130.x.y where x
and y are 8-bit numbers. When your device connects to our
network, it gets assigned one of those IP addresses.
How many devices can connect to the Wellesley network before we run out of IP addresses?
- 1,000,000
- 256
- 216
- none of the above
Bits and Color
Next time, we'll learn about colors, color primaries, and representations of colors. It will turn out that computers almost always use 24 bits to represent a color.
Quiz Question Nr. 8
How many colors is that?
- 1024
- 224
- 24,000
- 24,000,000
Solutions
Will be posted later, visit again after .
1. C. BLU is not part of the computer. 2. A. The clock determines the speed of the processor 3. D. The binary equivalent of 5 is 101 4. D. The decimal equivalent of 1010 is 10. 5. C. The ASCII character 67 is "C" 6. B. Since 2^10 = 1024, 10 bits sufficient to represent 1,000 7. C. two 8 bit numbers is the same as a 16-bit number, so 2^16 8. B 24-bit color means 2^24 colors